Rayleigh Quotient Graph Neural Networks for Graph-level Anomaly Detection Detection
Rayleigh Quotient Graph Neural Networks for Graph-level Anomaly Detection
文献地址:Rayleigh Quotient Graph Neural Networks for Graph-level Anomaly Detection | OpenReview
代码仓库:xydong127/RQGNN
1 问题
核心问题是:如何通过光谱特性有效地进行图级异常检测。
1.1 现有问题
- 光谱特性的忽视:
- 当前图异常检测方法多基于空间域的特征,例如节点属性和拓扑信息,未能充分利用图的光谱特性。
- 异常图和正常图在光谱能量分布上存在显著差异,但这一特性尚未被现有方法利用。
- 模型解释性不足:
- 许多现有方法框架复杂,设计上缺乏理论依据,难以解释异常检测的核心原理。
- 性能不足:
- 当前模型在异常检测任务中效果有限,特别是在数据不平衡的情况下难以有效捕捉异常模式。
1.2 文献中的解决方案
针对上述问题,本文提出了一个创新性的解决方案:
- 通过研究Rayleigh商,揭示正常图和异常图的累积光谱能量分布存在统计学差异。
- 利用光谱图神经网络(Spectral GNN)结合Rayleigh商进行显式与隐式学习,捕捉异常图的光谱特性。
- 通过提出Rayleigh Quotient Graph Neural Network(RQGNN),实现异常检测任务的高效和解释性解决方案。
1.3 目标
- 探索图的光谱特性:利用Rayleigh商描述光谱能量分布差异,为异常检测提供理论支持。
- 提高检测精度:设计能够捕捉异常图特征的高效模型,在多个真实世界数据集上验证其性能。
- 增强模型解释性:通过光谱特性(Rayleigh商)和模块化设计,提供异常检测的可解释框架。
文献的主要贡献在于首次将Rayleigh商引入到图级异常检测中,开辟了基于光谱特性的图异常检测新方向。
2 背景知识介绍
2.1 图的光谱特性
图的光谱特性是基于图的拉普拉斯矩阵或邻接矩阵的特征值和特征向量来描述图的全局结构、局部模式及其信号传播特性。它们广泛用于图分割、图嵌入、图信号处理等任务。
1. 图谱分析的基础
(1) 拉普拉斯矩阵
对于一个无向图 (G = (V, E)),拉普拉斯矩阵定义为:
其中:
- 是节点的度矩阵(对角元素为节点度数);
- 是邻接矩阵。
(2) 归一化拉普拉斯矩阵
归一化形式可以是:
(3) 谱分解
拉普拉斯矩阵 可以分解为:
其中:
- 是特征向量组成的矩阵;
- 是特征值对角矩阵,特征值按升序排列。
(4) 特征值的性质
- 且对应的特征向量为常数向量(全1向量),反映图的全局平滑性。
- 较小的特征值对应图的低频信息(平滑信号)。
- 较大的特征值对应图的高频信息(局部变化)。
2. 光谱特性描述图的几种方式
(1) 连通性
- 第二小特征值(Fiedler值) 表示图的连通性。
- :图是不连通的;
- :图是连通的,值越大表明连通性越强。
(2) 信号平滑性
- 光谱特性可以描述图上的信号传播特性。
- 低频信号:小特征值对应的特征向量反映了全局一致性信号。
- 高频信号:大特征值对应的特征向量捕捉了图中的局部变化或噪声。
(3) 图的全局结构
- 特征值分布反映了图的全局几何性质,例如节点的聚集度或离散度。
(4) 图的社区结构
- 社区检测任务可以利用特征值和特征向量:
- 特征值反映社区的连通性;
- 特征向量可以划分图为若干子图。
3. 图谱特性在不同任务中的意义
(1) 图分割
通过拉普拉斯矩阵的第二小特征值 和对应的特征向量,可以实现图的二分。
- 目标是找到一个切割,使得子图内部的连接紧密,子图之间的连接稀疏。
(2) 图信号处理
- 图上的信号(例如节点特征)可以被分解到不同频率域:
- 低频分量:全局一致性,类似平滑变化;
- 高频分量:局部剧烈变化或异常信号。
(3) 图嵌入
- 通过谱分解将图嵌入到低维空间,同时保留图的全局结构。
- 特征向量为嵌入向量,特征值用于度量不同分量的重要性。
(4) 图异常检测
- 异常图通常表现为高频信号(较大的特征值),因为异常会打破图的全局结构,增加局部变化。
(5) 传播特性分析
- 特征值的分布决定了图上信息扩散或传播的速度:
- 紧凑的特征值分布表示传播快;
- 分散的特征值分布表示传播慢。
4. 图光谱特性与Rayleigh商的关系
Rayleigh商为分析光谱特性提供了一个直观的度量工具:
其中:
- 是信号;
- 是拉普拉斯矩阵。
(1) 平滑性度量
- 的值越小,信号越平滑(低频分量多)。
- 的值越大,信号越不平滑(高频分量多)。
(2) 特征值与信号
- Rayleigh商的极值对应于拉普拉斯矩阵的特征值。
- 对应的信号 是拉普拉斯矩阵的特征向量。
5. 总结
图的光谱特性通过拉普拉斯矩阵的特征值和特征向量揭示了图的全局结构、信号传播模式和局部变化。特征值分布反映了图的连通性、平滑性和社区结构等重要性质。这些特性在图分割、嵌入、异常检测和传播分析等任务中具有广泛应用。Rayleigh商则提供了量化这些光谱特性的工具,是研究光谱特性的重要理论基础。
2.2 GNN发展
图神经网络(GNN)的发展与图的光谱特征密切相关,但并不仅仅依赖光谱特征。GNN的发展结合了光谱方法和空间方法,根据应用需求和计算效率逐步演进。
1. 基于光谱特征的GNN发展
早期的GNN模型主要受到图谱分析的启发,利用图的光谱特性设计过滤器或特征提取方法。
(1) 光谱图神经网络的基础
光谱图神经网络(Spectral GNN)以图的拉普拉斯矩阵的特征值和特征向量为基础,进行特征学习。
目标:
- 利用图的光谱特性捕捉全局信息。
- 通过滤波器处理图信号,实现节点或图的特征表示。
关键公式:
图信号在拉普拉斯矩阵上的过滤操作可以表示为:其中:
- 是拉普拉斯矩阵;
- 是拉普拉斯矩阵的特征向量矩阵;
- 是拉普拉斯矩阵的特征值对角矩阵;
- 是基于特征值设计的滤波器。
(2) 光谱GNN的代表方法
Spectral Convolutional Neural Networks (Bruna et al., 2013):
- 基于光谱域设计卷积操作,直接依赖拉普拉斯矩阵的特征分解。
- 缺点:特征分解的计算复杂度高,难以扩展到大规模图。
ChebNet (Defferrard et al., 2016):
- 使用切比雪夫多项式近似滤波器,减少了依赖拉普拉斯分解的计算。
- 滤波器表示为:其中是切比雪夫多项式,是归一化的拉普拉斯矩阵。
GCN (Graph Convolutional Networks, Kipf and Welling, 2017):
GCN进一步简化了光谱卷积,使用一阶近似,避免复杂的多项式计算:
其中:
- 是加自环的邻接矩阵;
- 是节点的度矩阵。
通过简化的图卷积操作,将光谱方法引入空间域。
光谱方法的局限性:
- 高计算成本:需要对图的拉普拉斯矩阵进行特征分解,计算复杂度高。
- 转移性差:光谱特性依赖于图的特定拓扑结构,难以泛化到不同图。
2. 空间域方法的发展
由于光谱方法的局限性,GNN逐步转向空间域方法,这类方法直接在节点的局部邻域上进行操作,无需特征分解。
(1) 空间域的核心思想
空间域方法将卷积操作转化为邻域信息的聚合,即通过每个节点的邻居信息生成节点的特征。
(2) 代表模型
GraphSAGE (Hamilton et al., 2017):
- 通过采样邻居节点,设计不同的聚合函数(如均值、最大值)进行特征更新:其中表示节点的邻居。
GAT (Graph Attention Networks, Velickovic et al., 2018):
- 引入注意力机制,根据邻居的重要性分配不同权重:其中是注意力权重。
Graph Isomorphism Network (GIN, Xu et al., 2019):
- 设计了一种强表达能力的聚合函数,理论上等价于 Weisfeiler-Lehman 图同构测试。
3. 光谱特征与空间特征的结合
近年来,研究者尝试结合光谱和空间方法,以更好地利用图的全局和局部信息。
(1) 光谱与空间的统一
例如:
SIGN (Scalable Inception Graph Networks, Rossi et al., 2020):
- 预先计算光谱特性,将其作为额外特征输入空间域方法。
ARMA (Atwood et al., 2020):
- 在图的频谱域和空间域之间交替优化,达到更好的性能。
(2) 高效的光谱方法
例如本文提到的Chebyshev波动滤波器,通过多项式近似实现光谱特性的高效学习。
3. 瑞利商的研究
作者通过系统分析和设计,创新性地使用了瑞利商(Rayleigh Quotient),以捕捉图的光谱特性,并结合其统计模式差异用于图级异常检测。以下是作者使用瑞利商的详细方法和步骤:
1. 理论基础:瑞利商与光谱能量分布
作者将瑞利商用于描述图的累积光谱能量分布,并揭示了正常图和异常图的能量分布差异:
瑞利商的定义为:
其中:
- 是图信号(如节点属性或结构特征);
- 是图的拉普拉斯矩阵。
累积光谱能量:
作者通过理论分析证明,瑞利商值可以直接量化图信号在低频和高频分量上的分布:- 小的瑞利商值对应低频能量(信号平滑,图的全局模式)。
- 大的瑞利商值对应高频能量(局部变化或异常)。
2. 瑞利商在异常检测中的发现
作者通过实验和理论发现:
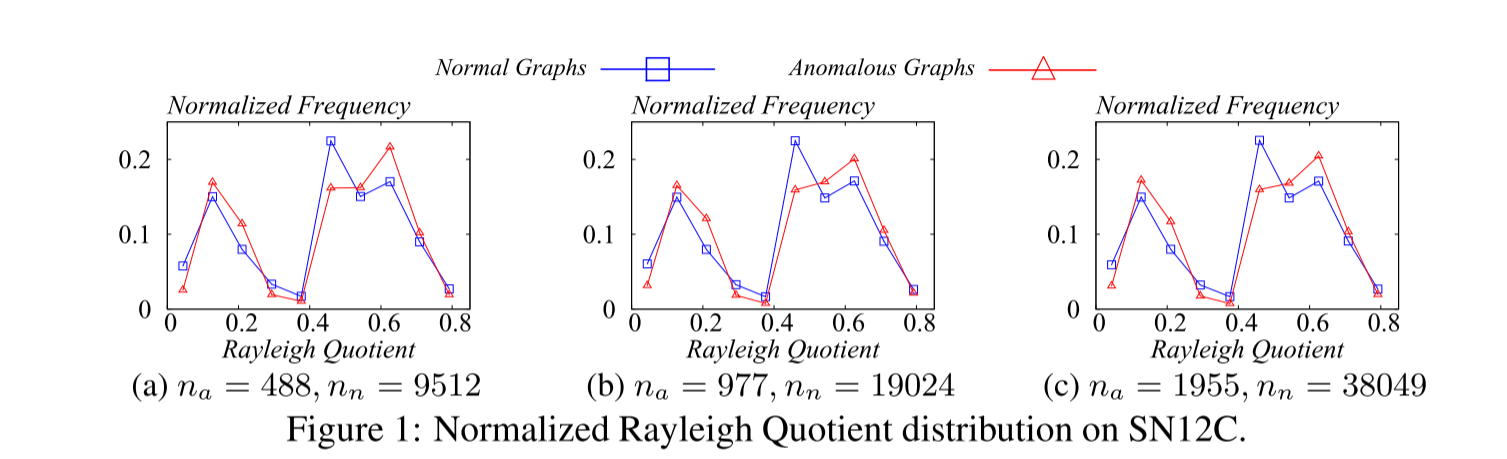
- 正常图的累积光谱能量分布倾向于低频,表现为较小的瑞利商值;
- 异常图的光谱能量更多分布在高频区域,导致瑞利商值较大。
这一模式差异为异常检测提供了新的依据。
3 方法
3.1 Rayleigh Quotient and Spectral Analysis 详细介绍:
核心内容:作者在这一节中通过理论分析,揭示了瑞利商在图谱分析中的作用,并探讨其与累积光谱能量分布的关系。这一部分为后续设计方法中的瑞利商学习组件(RQL)和光谱相关组件奠定了理论基础。
1. 瑞利商的定义与变化特性
瑞利商公式:
其中:
- :图的拉普拉斯矩阵;
- :图信号向量。
瑞利商用于衡量图信号在图结构上的光谱能量分布。
变化特性分析:
作者从理论上分析了瑞利商在拉普拉斯矩阵 或信号 存在小扰动时的变化范围:
定理1(拉普拉斯矩阵扰动):
对于任意图 ,若拉普拉斯矩阵存在扰动 ,瑞利商的变化范围满足:其中 是扰动矩阵的二范数。
定理2(信号扰动):
对于任意图 ,若图信号存在扰动 ,瑞利商的变化范围满足:当 足够小时,忽略高阶项后有:
启示:如果两个图的 和 足够接近,那么它们的瑞利商值也非常接近,从而可以用于相似性度量和类别划分。
2. 瑞利商与光谱能量分布
累积光谱能量表示:
累积光谱能量从 到 定义为:
其中:
- 是图信号在第 个特征值对应特征向量上的分量。
作者指出,通过累积光谱能量,可以衡量信号的频率分布。
瑞利商的转换:
- 作者证明累积光谱能量可以通过瑞利商表示,从而避免高成本的矩阵分解操作:其中 是光谱能量分布函数。
意义:瑞利商成为描述图光谱能量分布的一个高效替代方式。
3. 动机与指导
瑞利商分布模式:
- 正常图与异常图在瑞利商分布上的统计模式差异为异常检测提供了理论依据;
- 类别标签相同的图,其瑞利商值在不同样本中表现出一致性。
框架设计动机:
- 显式瑞利商学习:设计一个模块直接学习图的瑞利商值(第3.2节的RQL)。
- 光谱信息提取:结合光谱GNN捕捉累积光谱能量信息(第3.3节)。
总结
第3.1节从理论层面明确了瑞利商的变化特性及其与光谱能量的关系,展示了瑞利商作为图光谱特性指标的有效性。这些分析为后续模块设计提供了理论支持,同时证明了瑞利商在图异常检测中的潜力。
3.2. Rayleigh Quotient Learning Component (RQL)
作者详细介绍了如何通过设计一个专门的组件来显式学习图的瑞利商 (Rayleigh Quotient),以捕捉其光谱特性。
3.2.1. RQL 的设计目标
- 核心目标:直接从图数据中学习瑞利商特征,将其作为图的全局表示,用于后续的异常检测任务。
- 动机:瑞利商在正常图和异常图之间存在显著分布差异,这种差异可以作为分类的重要依据。
3.2.2. RQL 的工作流程**
RQL 模块通过以下步骤生成每个图的瑞利商表示:
输入:
- 图信号 ,表示图 中节点的属性矩阵;
- 图的拉普拉斯矩阵 。
- 处理步骤:
- 信号预处理:
使用多层感知机(MLP)对图信号进行变换:生成的 是变换后的节点信号矩阵。 - 瑞利商计算:
根据定义公式计算每个图的瑞利商:其中 表示提取对角元素。 - 高层表示提取:
再次通过 MLP 将瑞利商映射为全局特征:得到每个图的瑞利商特征表示。
- 信号预处理:
- 输出:
- ,即每个图的全局瑞利商表示。
3.2.3. 模块的优势
- 显式学习瑞利商:
直接量化图的光谱特性,避免复杂的光谱分解计算。 - 紧密结合光谱能量分布:
瑞利商有效反映了图信号在高频和低频区域的能量分布,为分类提供有力特征。 - 高效计算:
相比传统的图光谱方法,RQL 模块通过简单的矩阵操作和 MLP 映射实现高效计算。
3.2.4. RQL 在整体框架中的作用
- RQL 模块是 RQGNN 框架的第一部分,它的任务是生成图的显式瑞利商特征;
- 与后续隐式学习模块 (CWGNN with RQ-pooling) 结合,构成完整的异常检测框架。
3.3 Chebyshev Wavelet GNN with RQ-Pooling
核心内容:作者在这一节中提出了一个结合 Chebyshev波滤波器 和 RQ-Pooling(基于瑞利商的池化) 的模块,用于隐式学习图的光谱特性。这个模块能够捕获图的局部和全局信息,同时通过池化聚焦于图的关键区域。
3.3.1. Chebyshev Wavelet GNN
(1) 背景:光谱卷积的挑战
传统的光谱卷积(基于拉普拉斯矩阵特征值和特征向量)计算代价昂贵,尤其对于大规模图。为此,作者采用了 Chebyshev多项式近似,高效地实现频谱域上的图卷积操作。
(2) Chebyshev多项式卷积公式
给定图的归一化拉普拉斯矩阵 ,Chebyshev多项式定义为:
其中:
- ;
- 。
Chebyshev卷积通过多项式逼近拉普拉斯矩阵的特征值滤波器:
其中:
- 是需要学习的权重;
- 是 Chebyshev多项式。
(3) 实现
代码中,Chebyshev多项式卷积作用于每个节点的特征,通过累积多项式阶次捕获不同频段的频谱信息。
3.3.2. RQ-Pooling(基于瑞利商的池化)
(1) 背景:池化在图中的作用
池化操作是图级任务的重要步骤,能够在保留图全局特性的同时减少计算量。作者结合瑞利商的特性,引入 RQ-Pooling,用于选择对全局光谱特性贡献最大的节点区域。
(2) 瑞利商的注意力机制
通过瑞利商 计算每个节点的重要性分数:
其中:
- 是节点 对应的瑞利商值;
- 表示节点的重要性权重。
(3) 聚合节点特征
使用瑞利商权重聚合节点特征:
其中:
- 是节点 的隐式特征。
(4) 输出
池化后生成图的全局特征表示 。
3.3.3. 综合模块设计
作者将 Chebyshev Wavelet 和 RQ-Pooling 结合,实现隐式学习和池化的高效框架。
节点特征生成
通过 Chebyshev多项式卷积生成节点特征:
其中 是第 阶 Chebyshev滤波器。
基于瑞利商的池化
通过 RQ-Pooling 提取重要节点的特征并聚合成全局表示。
图的最终特征
将显式瑞利商特征和隐式光谱特征拼接:
3.3.4. 本节的关键创新
高效光谱卷积:
- 使用 Chebyshev多项式近似,降低了传统光谱卷积的计算复杂度;
- 捕获了图信号的多频段信息。
基于瑞利商的池化:
- 将瑞利商值引入注意力机制,为池化操作提供物理意义明确的权重;
- 强调高频和低频特性对全局图表示的不同贡献。
隐式与显式结合:
- 隐式特征通过卷积提取,显式特征通过瑞利商直接计算,形成互补。
3.4 Class-Balanced Focal Loss (CB Loss)
文献的第3.4部分提出了一种改进的损失函数——Class-Balanced Focal Loss (CB Loss),主要用于解决类别不平衡问题,特别是在异常检测任务中,正负样本比例差异可能导致模型偏向多数类别。
3.4.1. 动机
在异常检测任务中:
- 正常图(多数类)占据绝大多数,而异常图(少数类)数量有限。
- 常规交叉熵损失容易被多数类主导,导致模型无法有效学习少数类的特征。
- 作者引入类别平衡和焦点调整的策略,解决上述问题。
3.4.2. CB Loss 设计原理
(1) 类别平衡因子
通过类别样本数量计算有效样本数量(Effective Number of Samples):
其中:
- 是类别的样本数量;
- 是控制因子,。
类别权重:
(2) 焦点调整因子
焦点调整因子通过调节简单样本和困难样本的损失权重:
其中:
- 是预测概率;
- 是调节因子,控制困难样本的权重。
(3) 最终损失函数
CB Loss 的形式:
其中:
- 是样本总数;
- 是第 个样本的预测概率。
3.4.3. 优势分析
- 类别平衡:CB Loss 根据类别样本数量动态调整权重,显著降低了多数类的主导作用。
- 焦点调整:对错误预测的困难样本给予更大权重,提升了少数类样本的学习能力。
- 鲁棒性:在类别分布高度不平衡的情况下,CB Loss 能够提高模型对少数类的泛化能力。