Partitioning Message Passing for Graph Fraud Detection
文献地址:PMP.pdf
代码仓库:Xtra-Computing/PMP
1.背景及创新点
1. 问题背景与挑战
在使用图神经网络进行图欺诈检测时,主要面临两个挑战:
标签不平衡(Label Imbalance)
图数据通常存在标签不平衡的问题,即欺诈和非欺诈的节点标签数量差异很大。例如,在一个社交网络中,可能大多数节点代表的是正常用户,只有少部分节点代表欺诈用户。这种不平衡的标签分布会导致模型对少数类(欺诈类)预测不准确,从而影响整体检测效果。
同质性-异质性混合(Homophily-Heterophily Mixture)
图数据中存在着同质性(Homophily)和异质性(Heterophily)的混合关系:
- 同质性指的是图中节点之间具有相似的属性或标签,通常是图神经网络的假设基础(例如,社交网络中的好友节点往往有相似的兴趣)。
- 异质性则指的是图中某些节点之间存在明显的差异,例如不同类别或标签的节点连接在一起。
传统的图神经网络模型倾向于利用同质性关系,忽略异质性节点的贡献,但在实际的图欺诈检测任务中,异质性节点的信息同样重要,因为欺诈节点往往和非欺诈节点之间有着不同的行为模式或特征。
2. 现有方法的不足
当前大多数基于GNN的图欺诈检测模型倾向于通过“排除”异质邻居(即标签不同的节点)来增强模型的同质性假设,认为这样能够提高模型的预测准确性。然而,这种方法忽略了异质邻居中可能包含的有价值信息。特别是在图欺诈检测任务中,欺诈节点与正常节点之间的差异性可能正是模型检测欺诈行为的关键。
3. 创新点
In this paper, we argue that complicated trainable or predetermined strategies for excluding het-erophilic neighbors are unnecessary. Instead, the key of applying GNNs on fraud graphs is to distinguish neighbors during the message passing process, rather than exclusion. A powerful modelshould inherently have the capacity to adaptively modulate the information derived from both ho-mophilic and heterophilic neighbors.
在本文中,我们认为排除异质性邻居的复杂可训练或预定策略是没有必要的。相反,将GNN应用于欺诈图的关键是在消息传递过程中区分邻居,而不是排除。一个强大的模型应该本身具备适应性地调节来自同质性和异质性邻居信息的能力。
在PMP的邻居聚合阶段,采用不同的聚合函数分别处理同质性和异质性邻居。这确保了参数共享仅限于同一类别的节点,从而防止梯度被多数类别节点主导。对于类别未知的邻居,我们将它们的聚合函数配置为同标签邻居聚合函数的灵活组合,组合权重由与中心节点相关的适应性标量函数决定。
此外,由于欺诈图是同质性-异质性混合的,不同节点从同质性邻居和异质性邻居获得的信息量应根据节点的不同而适应性调整。为此将聚合函数的参数矩阵视为相对于中心节点的权重生成器的输出。这样每个节点可以在不增加额外参数的情况下,适应性地调整来自不同类别邻居的影响。
理论分析证明,PMP可被解释为节点特定的谱卷积,即每个节点拥有自己的谱图滤波器。与统一的图滤波器相比,这种方法更适合具有同质性和异质性混合的图,因为统一图滤波器无法平衡两者。
2.方法
1. PMP方法的基本构思
PMP方法的核心思想是将邻居根据类别(欺诈、良性、未标记)进行区分,并为不同类别的邻居采用不同的聚合函数。这种方法通过区分邻居类别来防止标签不平衡问题,避免良性节点对梯度的主导作用,从而增强模型对少数类别(如欺诈节点)的学习能力。
- 欺诈邻居:通过聚合函数 来处理。
- 良性邻居:通过聚合函数 来处理。
- 未标记邻居:通过灵活的聚合函数 来处理。
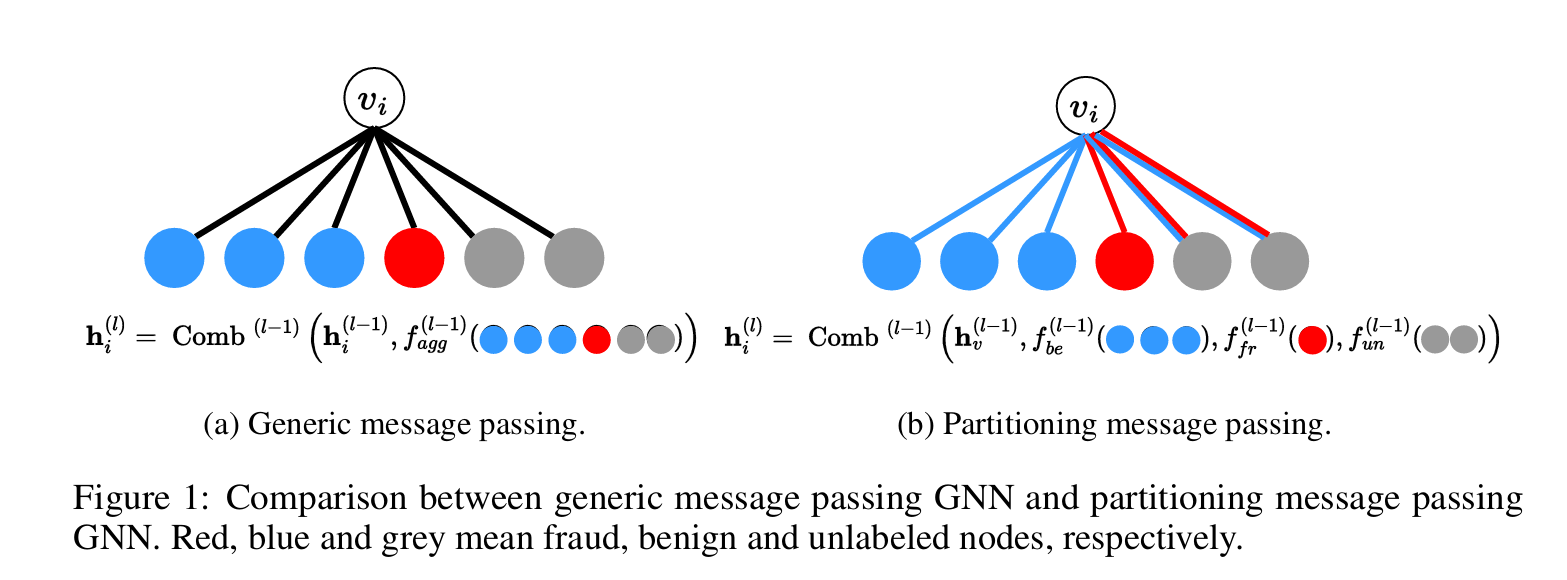
2. 消息传递过程
在第 层的消息传递过程中,PMP的操作通过以下公式进行:
其中:
- 表示节点 在第 层的隐藏表示。
- Comb 是一个组合函数,将自节点的特征和聚合的邻居消息结合起来。
- 是节点 在第 层的自特征。
- 分别是处理欺诈、良性和未标记邻居信息的聚合函数。
这种方式使得每个邻居类别(欺诈、良性、未标记)有独立的聚合函数,减少了标签不平衡问题,尤其避免了良性节点对梯度的主导作用。
3. 未标记邻居的处理
对于未标记邻居,PMP采用了一种加权组合的方式进行处理。
其中, 是一个自适应标量,控制未标记邻居与欺诈邻居或良性邻居的相似度。具体来说:
- 当 较大时,未标记邻居更倾向于被视为欺诈节点。
- 当 较小时,未标记邻居更倾向于被视为良性节点。
该标量 是通过以下公式计算的:
- 是一个单层的多层感知机(MLP)函数,输入为节点 的隐藏特征 ,输出为一个标量 ,表示未标记邻居的标签倾向。
通过这种方法,PMP可以动态地调整未标记邻居的处理方式,而不是硬性地对其赋予一个固定标签,能够灵活地处理不确定的连接。
4. 自适应权重生成
PMP方法通过为每个节点生成特定的权重矩阵,使得每个节点的邻居信息聚合具有自适应性。具体来说,针对每个节点 ,聚合函数使用的权重矩阵 和 不是固定的,而是通过基于节点特征生成的学习型权重矩阵来调整。公式如下:
- 和 是两个单层的MLP模型,用于生成节点特定的权重矩阵。
- 这些权重矩阵是动态生成的,确保模型可以根据每个节点的特征适应性地调整对不同类别邻居的影响。
这种基于节点特征生成权重矩阵的方式,避免了传统方法中使用共享权重矩阵的弊端,从而使得每个节点能够更好地适应其特定的邻居结构。
5. 谱图卷积的解释
PMP通过谱图卷积的视角解释其模型行为。每个节点的消息传递过程可以看作是一个自适应的谱图卷积操作,具体为:
- 和 是分别针对欺诈邻居和良性邻居的谱图卷积滤波器。
- 是节点特征矩阵, 和 是对应的权重矩阵。
- 是归一化的拉普拉斯矩阵,用于表示图的结构。
PMP确保每个节点都有一个专属的谱图滤波器,这意味着每个节点能够根据其具体的图结构背景来适应性地处理邻居的信息。这种方法优于传统的统一图滤波器,因为它能够更好地处理图中的同质性和异质性混合。
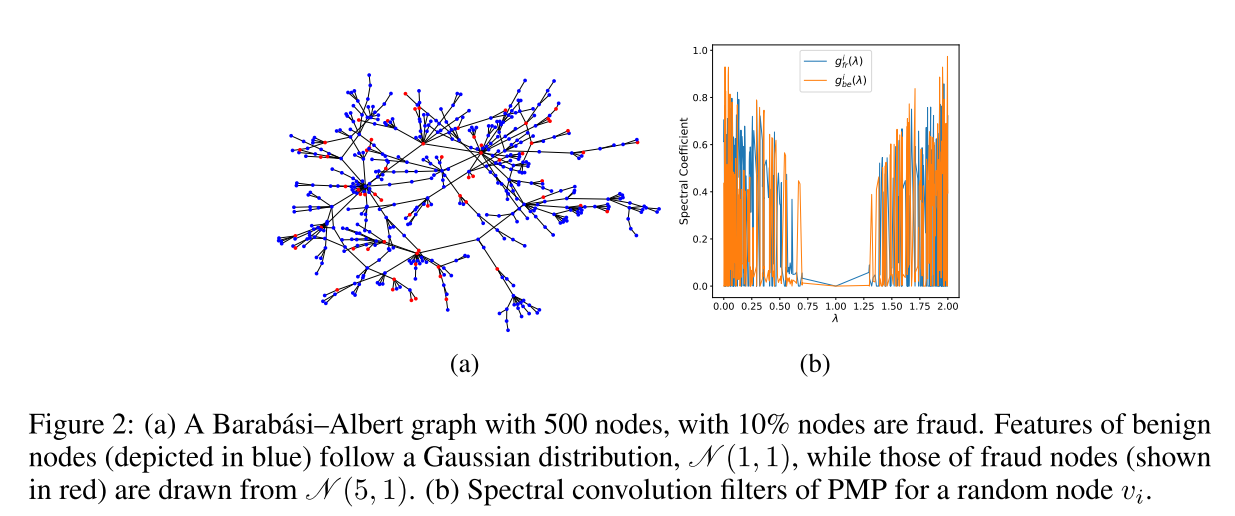
图展示了PMP方法在Barabási–Albert图上的实验结果,包括以下两部分:
(a) 图结构
这是一个包含500个节点的Barabási–Albert图,其中10%的节点为欺诈节点(红色表示),90%的节点为良性节点(蓝色表示)。节点的特征分布如下:
- 良性节点的特征服从高斯分布 。
- 欺诈节点的特征服从高斯分布 。
这部分展示了良性和欺诈节点在网络中的混合情况,强调了同质性(良性节点聚集)和异质性(欺诈节点与良性节点混合)的共存。
(b) 谱卷积滤波器
这部分展示了PMP方法针对一个随机节点 的谱卷积滤波器 和 的频谱响应:
- 蓝色曲线: 表示欺诈邻居的滤波器响应。
- 橙色曲线: 表示良性邻居的滤波器响应。
可以看到,两个滤波器在频域内互为补充,分别覆盖了不同的频率范围。这种设计确保了PMP能够针对不同类别的邻居信息进行区分和处理,从而适应同质性和异质性混合的图结构。